Sean Carroll: Quantum Mechanics and the Many-Worlds Interpretation | Lex Fridman Podcast #47 | Summary and Q&A

TL;DR

Sean Carroll delves into quantum mechanics and the intriguing concept of the many-worlds interpretation, providing insight into the fundamental nature of reality.

Key Insights

• 🤨 Classical mechanics raised concerns about action at a distance, which led to the development of the gravitational field theory.
• 👾 The concept of Hilbert space characterizes the amount of information needed to describe the state of a quantum system.
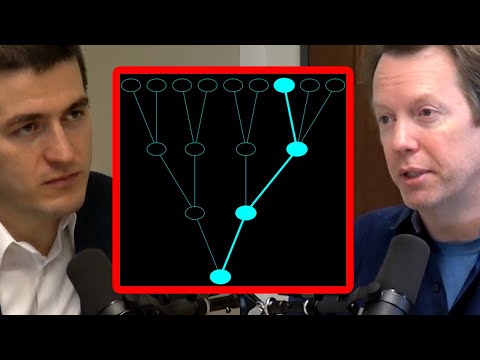
• 🌍 The many-worlds interpretation suggests that quantum systems split into separate branches, representing different observations or outcomes.
• 👻 Entanglement is a fundamental feature of quantum mechanics, allowing seemingly connected behavior between entangled particles.

Transcript

the following is a conversation with Sean Carroll part 2 the second time we've spoken on the podcast you can get the link to the first time in the description this time we focus on quantum mechanics and the many-worlds interpretation that he details elegantly in his new book titled something deeply hidden I own and enjoy both the ebook and audioboo... Read More

Questions & Answers

Q: How did classical mechanics lead to the development of the gravitational field theory?

Classical mechanics, developed by Isaac Newton, raised concerns about action at a distance, particularly with gravity. Pierre-Simon Laplace later showed that Newtonian gravity could be rewritten as a field theory, eliminating the need for direct action between distant objects.

Q: What is the many-worlds interpretation of quantum mechanics?

The many-worlds interpretation suggests that the universe splits into multiple distinct branches whenever a quantum system that is in a superposition becomes entangled with the outside world. Each branch represents a different outcome of the observation, giving rise to a multitude of parallel worlds.

Q: What is the significance of Hilbert space in quantum mechanics?

Hilbert space is an abstract mathematical space that represents all possible quantum wave functions for a specific system or the entire universe. The dimensions of Hilbert space indicate the amount of information needed to describe the system's state comprehensively.

Q: How does the concept of entanglement work in quantum mechanics?

Entanglement occurs when two or more quantum systems become correlated in such a way that the state of one system is dependent on the state of another. Observing one entangled system can provide information about the other, resulting in seemingly coordinated behavior, regardless of the distance between them.

Q: How did classical mechanics lead to the development of the gravitational field theory?

Classical mechanics, developed by Isaac Newton, raised concerns about action at a distance, particularly with gravity. Pierre-Simon Laplace later showed that Newtonian gravity could be rewritten as a field theory, eliminating the need for direct action between distant objects.

More Insights

• Classical mechanics raised concerns about action at a distance, which led to the development of the gravitational field theory.

• The concept of Hilbert space characterizes the amount of information needed to describe the state of a quantum system.

• The many-worlds interpretation suggests that quantum systems split into separate branches, representing different observations or outcomes.

• Entanglement is a fundamental feature of quantum mechanics, allowing seemingly connected behavior between entangled particles.

• Alternative interpretations of quantum mechanics include hidden variable theories, spontaneous collapse theories, and epistemic interpretations.

Summary

In this conversation, Sean Carroll discusses various aspects of quantum mechanics and the many-worlds interpretation. He explains classical mechanics and how it differs from quantum mechanics. He also talks about the concept of action at a distance, the nature of fields, and how general relativity addresses these issues. Carroll discusses the limits of human understanding and the relationship between math and physics. He also explores the fundamental ideas of conservation of momentum and the distinction between the world as it is and the world as we observe it. Finally, Carroll dives into the concepts of atoms, electrons, wave functions, entanglement, Hilbert space, dimensions, entropy, and infinity.

Questions & Answers

Q: What were some of the worries about classical mechanics?

One concern with classical mechanics was the concept of action at a distance, where objects could affect each other without physical contact. Another worry was how the Earth knew about the Sun's gravitational force from a distance.

Q: How did scientists address these concerns about classical mechanics?

Pierre-Simon Laplace showed that Newtonian gravity could be rewritten as a field theory, where there is a gravitational field that describes the force between the Sun and the Earth. Einstein's general relativity also introduced a field in space, with the speed of light as a limit for action.

Q: Is there a limit to our ability to understand the natural world?

While there may be limits to certain abilities, such as visualization or calculation, there is no clear limit to our understanding of the natural world. Our intuitions can be trained and developed to comprehend complex concepts, and history has repeatedly shown that we can continue to expand our understanding.

Q: What is the most beautiful idea in physics?

According to Sean Carroll, the conservation of momentum is the most beautiful idea in physics. It signifies a shift from viewing nature as having purposes and goals, to perceiving patterns in the world through laws and equations.

Q: What is the difference between math and physics?

Math is about the logical structure of all possible worlds, while physics focuses on our actual world. Although math is incredibly useful in constructing physical theories, it is the simplicity and power of math's application to the real world that is surprising.

Q: What is entanglement?

Entanglement is a fundamental concept in quantum mechanics. It refers to the correlation between two or more particles, such that measuring the state of one particle instantaneously affects the state of the other particles, regardless of distance. This feature is not observed in classical mechanics.

Q: What is Hilbert space, and how does it relate to Euclidean space?

Hilbert space is an abstract mathematical space that represents all possible quantum wave functions for a given system. It is often infinite-dimensional but can also be large and finite. Euclidean space, on the other hand, refers to the three-dimensional space in which we live.

Q: What is the relationship between dimensions in Hilbert space and the amount of information in a system?

Dimensions in Hilbert space represent the amount of information needed to describe the state of a system. The more numbers required, the more dimensions the Hilbert space has. This corresponds to the level of unknown information, or entropy, in the system.

Q: What is entropy in quantum mechanics?

Entropy is a measure of how much we don't know about the state of a system in relation to its full microscopic details. It characterizes the difference between what we know and what we don't know about a quantum system, in terms of its wave function or probabilities. The size of the Hilbert space determines the potential entropy of a system.

Q: How do we think about infinity in math and physics?

Infinity is a concept that can be manipulated mathematically, and we can define operational rules around it. However, comprehending infinity is challenging for our cognitive abilities. Although we can work with and understand the properties of infinity, it remains a concept that is difficult to fully grasp intuitively.

Takeaways

Sean Carroll provides insights into the concepts of classical mechanics, quantum mechanics, and the many-worlds interpretation. He explores the limits of human understanding, the relationship between math and physics, and the beauty of fundamental ideas like conservation of momentum. Carroll discusses atoms, electrons, wave functions, entanglement, Hilbert space, dimensions, entropy, and the abstract concept of infinity. While some of these concepts remain challenging, they play an essential role in our understanding of the natural world and the mysteries of the quantum realm.

Summary & Key Takeaways

• Sean Carroll discusses the history of classical mechanics and how it evolved to include the concept of action at a distance, leading to the development of the gravitational field theory.

• He explores the distinction between classical mechanics and quantum mechanics, with a focus on the wave function and its behavior in the many-worlds interpretation.

• Carroll explains the concept of Hilbert space in quantum mechanics and its connection to the dimensions of the system, as well as the notion of entanglement and its implications.