Banked turn Physics Problems | Summary and Q&A

TL;DR

Understanding the physics behind banked curves and how to calculate the speed required to prevent sliding.

Key Insights

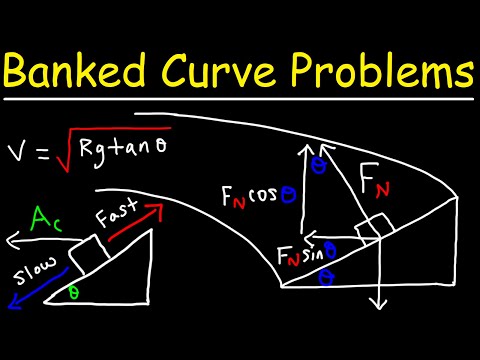
• 🐎 Banked curves involve circular motion and require a certain speed to prevent sliding up or down.
• 😨 The normal force in a banked curve is greater than on a regular incline, as it supports the weight of the car and provides the centripetal force.
• 🥰 The speed required can be calculated using the equation v = sqrt(rgtanθ).

Questions & Answers

Q: How does the normal force differ between a banked curve and a regular incline?

In a banked curve, the normal force supports more than just the weight of the car. It also provides the centripetal force required for circular motion. In contrast, a normal incline only supports a portion of the weight force.

Q: What happens if a car moves too fast on a banked curve without friction?

If the car exceeds the speed required for maintaining its position, it will slide up the banked curve. The force of gravity will not be enough to keep the car in place.

Q: What happens if a car moves too slow on a banked curve without friction?

If the car's speed is too slow, it will slide down towards the center of the banked curve. The centripetal force needed for circular motion will not be sufficient.

Q: How can one calculate the speed required to prevent sliding on a banked curve?

The speed can be calculated using the equation v = sqrt(rgtanθ), where r is the radius of curvature, g is the acceleration due to gravity, and θ is the angle of the banked curve.

Summary & Key Takeaways

• Banked curves involve circular motion, with a car moving on an inclined surface.

• The normal force in banked curves is greater than on regular inclines, as it supports the weight of the car and provides the centripetal force.

• The speed required for a car to maintain its position on a banked curve without sliding can be calculated using the equation v = sqrt(rgtanθ).